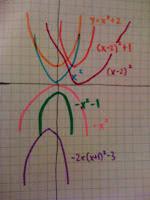
The Ch. 0 Graphing Functions Project demonstrated how there are several different transformations for each of the five parent functions.
The original parent function is y = |x|, shown in the dark teal. The vertical translation, y = |x| -1, is the blue graph. y=|x| is shifted vertically down by 1 unit. The horizontal translation, y= |x-5|, is the purple graph. y=|x| is shifted horizontally to the left by 5 units. The vertical & horizontal translation, y = |x-2|+4, is the red graph. y=|x| is shifted vertically 2 units to the right and shifted horizontally 4 units up. The horizontal reflection, y = -|x| , is the green graph. y=|x| is flipped across the x-axis, making both the functions symmetric. The vertical & horizontal translation & reflection, y = -|x-6|-7, is the pink graph. y=| x | is reflected across x-axis, shifted horizontally to the right 6 units, and shifted vertically down 7 units. The vertical shrink, y = -2|x-3|+1, is the darker pink graph. There is a reflection over x-axis, a horizontal shift to the right 3 units, a vertical shift up 1 unit, and a vertical shrink by -2.